Robots are no longer futuristic machines they are now working in warehouses, hospitals, and even homes. For a robot to function properly, it must know where it is in its environment. This process is called robot localization, and it is the foundation for advanced tasks like navigation, mapping, and motion planning.
In this beginner-friendly guide, we’ll explore how indoor robot localization works, why robot pose estimation is important, and how you can implement robot localization using encoder odometry in C++. Along the way, you’ll see equations, practical examples, and even a chart of robot parameters to help you visualize the process.
What is Robot Localization?
Simply put, robot localization is the ability of a robot to know its position (X, Y) and orientation (θ) inside an environment.
Imagine driving a car without GPS you would not know where you are on the road. Similarly, without localization, a robot cannot move intelligently. Localization enables tasks such as:
- Following a path in a factory.
- Avoiding obstacles while navigating.
- Performing SLAM (Simultaneous Localization and Mapping).
- Carrying out delivery missions indoors.
Primary benefit: Without robot localization, higher-level algorithms like motion planning or SLAM cannot work.
Why Indoor Robot Localization is Challenging
Unlike outdoor robots that can use GPS, indoor robots face different challenges, GPS doesn’t work indoors, and small errors in wheel rotation accumulate over time.
A practical example of these challenges is discussed in ROS Mapping and Localization
- GPS does not work indoors.
- Small errors in wheel rotation accumulate over time.
- Robots need to track their movement in real-time without external signals.
That’s why odometry using encoders is often the first step for indoor robot localization.
Components Needed for Robot Localization
A typical indoor mobile robot consists of:
- Microcontroller – acts as the brain.
- Motors and motor driver – generate movement.
- Wheels with encoders – measure wheel rotation.
- IMU (Inertial Measurement Unit) – measures tilt and acceleration.
- Battery – powers the system.
Encoders play a key role because they measure wheel rotations, which can be converted into distances.
Measuring Your Robot for Localization
Before applying equations, you must measure your robot’s physical parameters:
- Wheel base (distance between wheels): 17 cm
- Wheel radius: 3.25 cm
- Encoder ticks per revolution: Left = 370, Right = 380
Here’s a simple visualization of these robot parameters:
These values are used in localization equations to compute the robot’s position.
Odometry Equations for Robot Localization
Encoders provide ticks (rotations). These are converted into distances using:
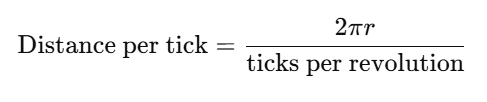
Next, we calculate:
- Distance Center (dCenter):
- Change in angle (dTheta):

Finally, update the pose of the robot:

This gives the robot’s pose estimation in the global frame.
Implementing Robot Localization Using Encoder Odometry in C++
Here’s a simple C++ program for odometry:
#include <iostream>
#include <cmath>
class DifferentialDriveOdometry {
public:
DifferentialDriveOdometry(double wheelRadius, double wheelBase, int ticksPerRevLeft, int ticksPerRevRight)
: r(wheelRadius), L(wheelBase), ticksLeft(ticksPerRevLeft), ticksRight(ticksPerRevRight),
x(0.0), y(0.0), theta(0.0), prevLeft(0), prevRight(0) {}
void update(int leftCount, int rightCount) {
int deltaLeft = leftCount - prevLeft;
int deltaRight = rightCount - prevRight;
prevLeft = leftCount;
prevRight = rightCount;
double distLeft = (2 * M_PI * r * deltaLeft) / ticksLeft;
double distRight = (2 * M_PI * r * deltaRight) / ticksRight;
double dCenter = (distLeft + distRight) / 2.0;
double dTheta = (distRight - distLeft) / L;
x += dCenter * cos(theta + dTheta / 2.0);
y += dCenter * sin(theta + dTheta / 2.0);
theta += dTheta;
if (theta > M_PI) theta -= 2 * M_PI;
if (theta < -M_PI) theta += 2 * M_PI;
}
void pose() {
std::cout << "X: " << x << " Y: " << y << " Theta: " << theta << std::endl;
}
private:
double r, L;
int ticksLeft, ticksRight;
double x, y, theta;
int prevLeft, prevRight;
};
int main() {
DifferentialDriveOdometry odom(0.0325, 0.17, 370, 380);
odom.update(100, 100);
odom.pose();
odom.update(200, 190);
odom.pose();
return 0;
}This code continuously updates the robot’s X, Y, and Theta as encoder values change.
Practical Challenges in Robot Localization
Even if the math is correct, robots face real-world issues:
- Wheel slip: friction causes drift.
- Uneven motors: left and right wheels may not rotate equally.
- Encoder mismatches: even identical encoders may output different tick counts.
Because of these issues, odometry alone is not enough. That’s why localization is often combined with IMUs, cameras, or LiDAR.
Beyond Encoders: Improving Localization
For advanced applications, robot localization is combined with:
- IMU fusion – for better orientation tracking.
- Vision-based localization – using cameras.
- SLAM algorithms – mapping while localizing.
A good starting point is odometry, but for reliable indoor navigation, additional sensors are recommended.
FAQs on Robot Localization
Q1: What is robot localization?
It is the process of finding a robot’s position and orientation in a given environment.
Q2: How does indoor robot localization work without GPS?
It relies on encoders, IMUs, and vision sensors instead of GPS.
Q3: What is robot pose estimation?
It means finding the X, Y coordinates and the orientation (theta) of a robot.
Q4: Why do we use encoder odometry in C++?
C++ is fast, reliable, and widely used in robotics frameworks like ROS.
Q5: Can robot localization be done with only odometry?
Yes, but errors accumulate. That’s why IMU or vision-based systems are usually added.
Conclusion
Robot localization is the foundation of indoor mobile robotics. By using encoders, odometry equations, and simple C++ programs, we can estimate a robot’s pose (X, Y, Theta). While odometry provides a great starting point, real-world challenges like drift and wheel slip require sensor fusion with IMUs or cameras.
If you’re building your first robot, start with encoder-based odometry, implement it in C++, and test it by moving forward and backward. Once you see the math come alive, you’ll realize how essential localization is for advanced robotics applications like navigation, motion planning, and SLAM.
